⯈Algorithm and its Characteristics
⯈Elementary Problems
- Addition of two numbers
- Calculate area and circumference of circle
- Calculate area of triangle
- Calculate simple interest
- Calculate slope and distance between two points
- Convert length in feet to inches
- Weighted score in exam
- Convert temperature in degree Celsius to Fahrenheit
- Swap two numbers
- Swap two numbers without using extra variable
- Overview of C Programming Language
- Getting started with C Programming Language
- Keywords
- Identifiers
- Constants
- Operators
- Expression Evaluation
- Mathematical expression to C equivalent expressions
- Datatypes
- Variables
- Integer representation in C
- Character representation in C
- Type conversion in C
- sizeof operator
- Comments
- Mathematical Functions
- input output statements
- width specifiers in C
- structure of a C program
- header files
- Compilation process of a C program
- Types of initializations.
⯈Basic C Programs
- C program to add two numbers
- C program to find area and circumference of circle
- C program to swap two numbers
- C program to swap two numbers without using extra variable
- C program to swap two numbers using bitwise XOR
- C program to convert temperature in Celsius to Fahrenheit
- C program to calculate gross salary of an employee
- C program to count number of digits in a positive integer
- C program to count number of digits in binary representation
- C program to count number of digits in base ‘K’
- C program to convert kilometer to meter, feet, inches and centimeters
- C program to find first and last digit of a number
- C program to find minimum number of currency denominations
- C program to convert cartesian coordinates to polar coordinates
- C program to find distance between two places on earth in nautical miles
- C program to find slope and distance between two points
- C program to add 1 to the number using ‘+’ operator
- C program to find maximum of two numbers using ternary operator
- C program to find maximum of three numbers using ternary operator
- C program to find kth bit of a number
- C program to find last four bits of a byte
- C Program to reset right most set bit of a number
Bitwise operators in C
The bitwise operators work on the bit pattern of the number. These operators can only be applied on the integers. It is highly advised that you study the base conversions before going through this tutorial.
Note: Even the shift operators that we have studied are bitwise operators. Here we will study the other bitwise operators.
You may refer to the video posted at the end of this page.
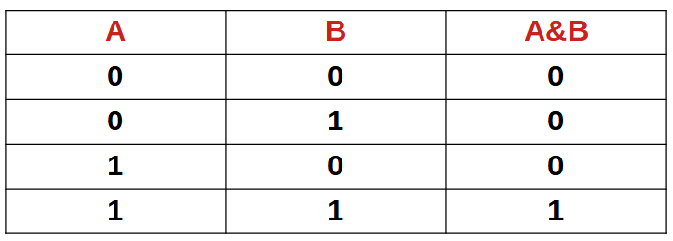
Bitwise AND (&)
- It is a binary operator.
- & is read as “ampersand“
Truth table for AND is,
Let us take examples and understand this operator.
y = 25 & 19
We convert 25 to binary and 19 to binary and take bit by bit AND value of it.
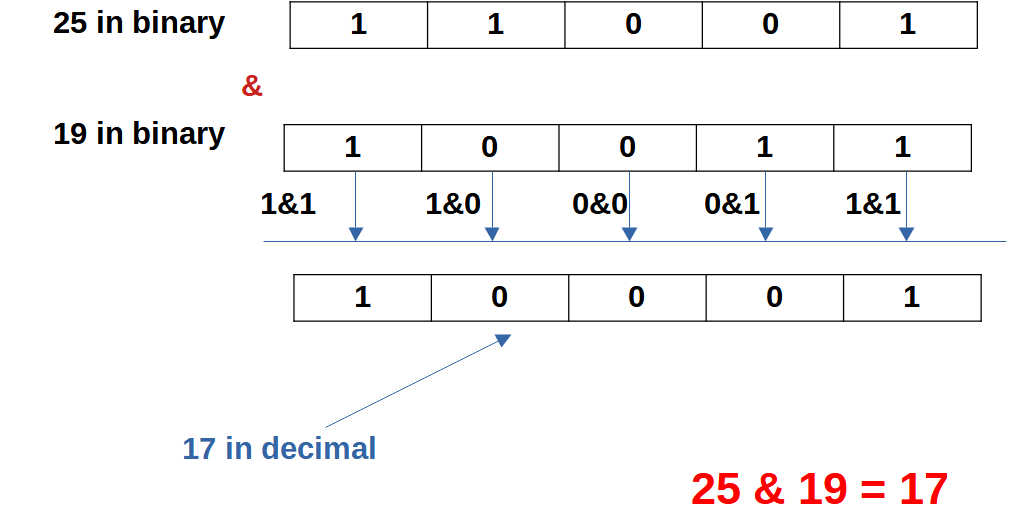
Therefore,
25 & 19 = 17
Note: We would have written all the 32 bits, since all the LHS bits from position 5 are 0, we ignore that, as it won't affect our answer.
What to do if both the number of different number of bits, we pad 0’s to make both the number to have equal number of bits.
Lets take an example and understand this.
y = 7 & 10
7 in binary is 111.
10 in binary is 1010.
Since 7 has three bits and 10 has four bits, we append 0 to 7, to make it as 4 bits.
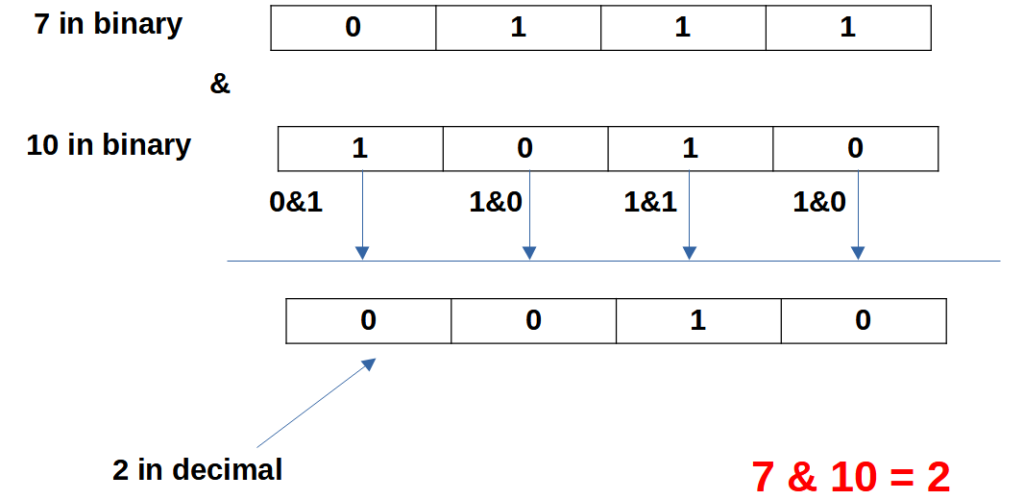
Therefore,
7& 10 = 2
-1 & -2 = -2
25 & -15 = 17
Note : Convert the negative numbers in 2’s complement form. If the result is negative (MSB is 1) then get the number back from 2’s complement. You may refer here or you may refer the negation operator discussed at the bottom of this page.
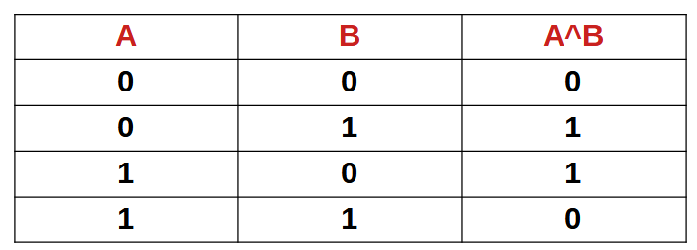
Bitwise XOR (^)
- It is a binary operator.
- ^ is read as “carat“
Truth table for XOR is,
Let us take examples and understand this operator.
y = 25 & 19
We convert 25 to binary and 19 to binary and take bit by bit XOR value of it.
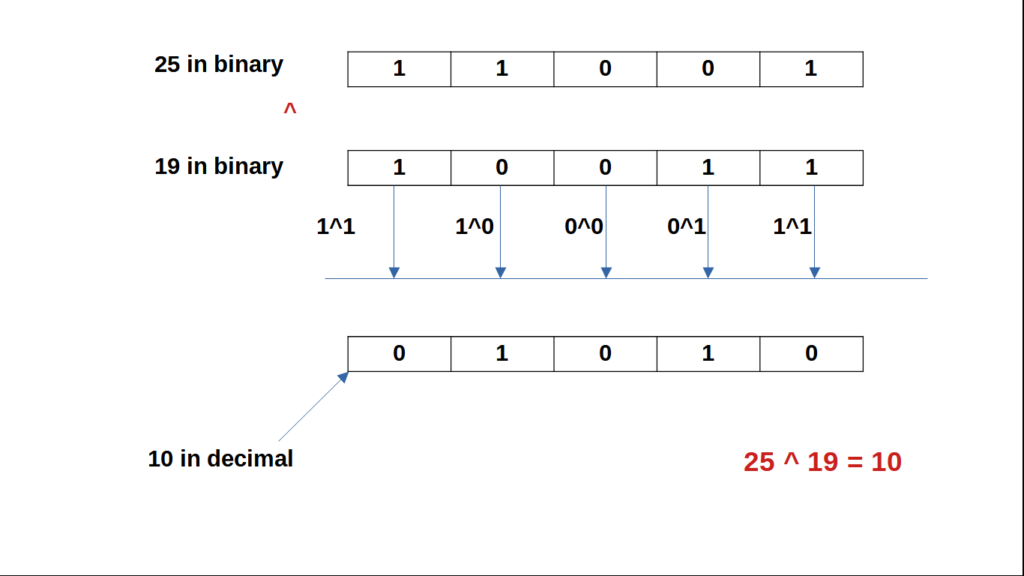
If the numbers have different bits, then we pad 0’s to make them of equal length and then take bitwise XOR.
Lets take an example and understand this.
y = 7 ^ 10
7 in binary is 111.
10 in binary is 1010.
Since 7 has three bits and 10 has four bits, we append 0 to 7, to make it as 4 bits.
If we perform 7 ^ 10 we get 13. (Do it yourself)
-1 ^ -2 = 1
25 ^ -15 = -24
Note : Convert the negative numbers in 2’s complement form. If the result is negative (MSB is 1) then get the number back from 2’s complement. You may refer here or you may refer the negation operator discussed at the bottom of this page.
Bitwise OR ( | )
- It is a binary operator.
- | is read as “pipe“
Truth table for OR is,
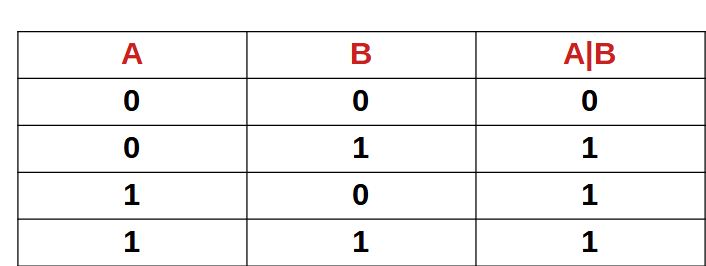
Let us take examples and understand this operator.
y = 25 | 19
We convert 25 to binary and 19 to binary and take bit by bit OR value of it.
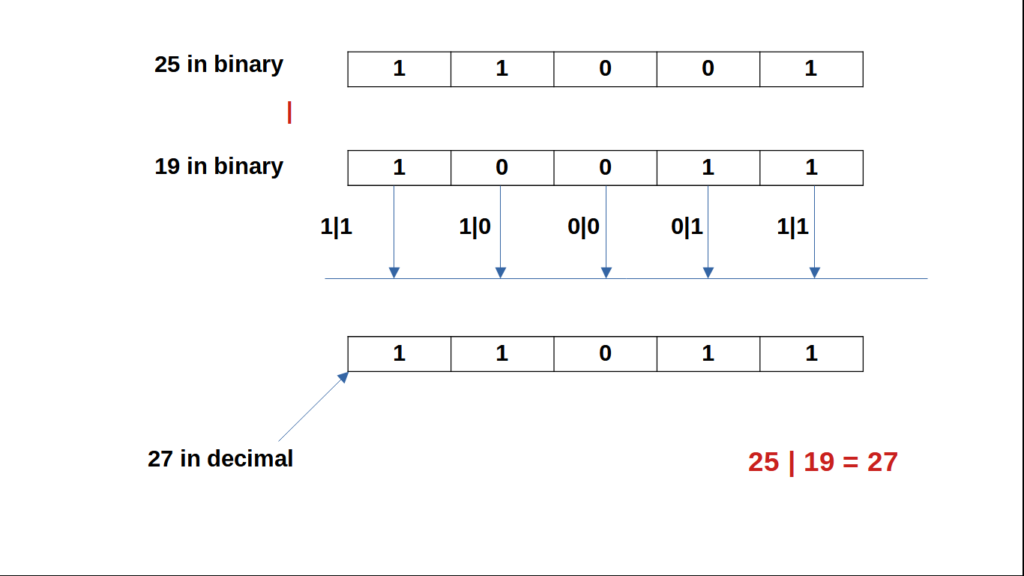
If the numbers have different bits, then we pad 0’s to make them of equal length and then take bitwise OR.
Lets take an example and understand this.
y = 7 | 10
7 in binary is 111.
10 in binary is 1010.
Since 7 has three bits and 10 has four bits, we append 0 to 7, to make it as 4 bits.
If we perform 7 | 10 we get 15. (Do it yourself)
-1 | -2 = -1
25 | -15 = -7
Note : Convert the negative numbers in 2’s complement form. If the result is negative (MSB is 1) then get the number back from 2’s complement. You may refer here or you may refer the negation operator discussed at the bottom of this page.
Negation (~)
- It is a unary operator.
- It flips the given bit pattern.
- If we get the MSB in answer as 1, it means that the number is negative, and we need to get back the number from 2’s complement.
Let us understand the negation operator with an example,
y = ~5
Here we convert 5 to binary and flip all the bits.
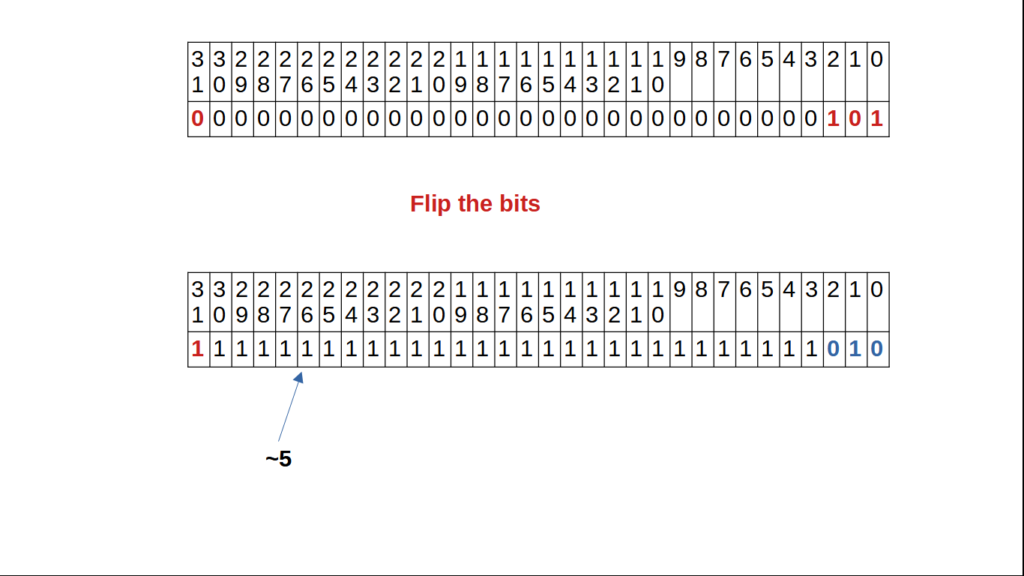
We see that the MSB of ~5 is 1, that means the number is negative. The negative number are stored in 2’s complement form. Hence, we need to get the original number from it. Therefore, the ~5, is in 2’s complement form.
The process,
- Get the 1’s complement from the 2’s complement number by subtracting 1.
- Invert all the bits to get the original number. (Don’t invert the MSB)

we see that the final answe has the bit pattern 110, which is 6, and MSB is 1. Therefore, ~5 = -6
In general, we can say,
~N = -(N+1)
Therefore,
~1 = -2
~(-5) = 6
